Pagina:Opere matematiche (Cremona) I.djvu/347

introduzione ad una teoria geometrica delle curve piane.

333

Suppongo ora che il polo $o$ coincida, insieme con $a_{n}\,a_{n-1}\dots a_{n-s+1}$, in un unico punto. Allora si ha:

$\sum (oa)_{n}=0,\quad \sum (oa)_{n-1}=0,\dots \sum (oa)_{n-s+1}=0$;

quindi l’equazione che precede riesce divisibile per ${\overline {om}}^{s}$, ossia il polo $o$ tien luogo di $s$ centri armonici di grado qualunque. Gli altri $r-s$ centri armonici, di grado $r$, sono dati dall’equazione:

${\overline {om}}^{r-s}\sum (oa)_{n-r}-(n-r+1){\overline {om}}^{r-s-1}\sum (oa)_{n-r+1}$ $+{\frac {(n-r+2)(n-r+1)}{1.2}}{\overline {om}}^{r-s-2}\sum (oa)_{n-r+2}\dots =0$,

ove le somme $\sum (oa)$ contengono solamente i punti $a_{1}\,a_{2}\dots a_{n-s}$. Dunque, gli altri $r-s$ punti $m$, che insieme ad $o$ preso $s$ volte costituiscono i centri armonici, di grado $r$, del sistema $a_{1}\,a_{2}\dots a_{n}$ rispetto al polo $o$, sono i centri armonici, di grado $r-s$, del sistema $a_{1}\,a_{2}\dots a_{n-s}$ rispetto allo stesso polo $o$¹.

Si noti poi che, per $s=r+1$, l’ultima equazione è sodisfatta identicamente, qualunque sia $m$. Cioè, se $r+1$ punti $a$ ed il polo $o$ coincidono insieme, i centri armonici del grado $r$ riescono indeterminati, onde potrà assumersi come tale un punto qualunque della retta $a_{1}\,a_{2}\dots$².

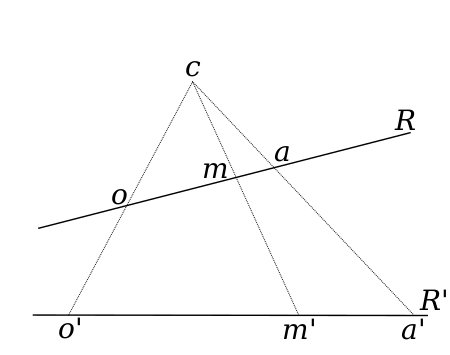18. Abbiasi, come sopra (11), in una retta $\mathrm {R}$ (fig. 5.^a) un sistema di $n$ punti $a_{1}\,a_{2}\dots a_{n}$Fig.ª 5.ªFig.ª 5.ª ed un polo $o$; sia inoltre $m$ un centro armonico di grado $r$, onde fra i segmenti $ma$,

---

1. {Viceversa, se $s$ centri armonici (di grado qualunque) coincidono nel polo $o$, in questo coincideranno $s$ punti del sistema fondamentale.}
2. {Viceversa, se i centri armonici di grado $r$ rispetto ad un polo $o$ sono indeterminati, i centri armonici di grado $r+1$ sono tutti riuniti in $o$, e questo punto in tal caso assorbe anche $r+1$ punti del sistema fondamentale.}