Pagina:Bonola - La geometria non-euclidea.djvu/36

— 28 —

Lo stesso ragionamento è applicabile nell'ipotesi

$E'F'=AB$.

Dimostriamo il 2° teorema.

Supponiamo in primo luogo $EF>AB$. Allora su $EF$ prendiamo $EI=AB$ e congiungiamo $I$ con $A$ e $C$. Valgono allora le seguenti relazioni.

Inoltre, pel teorema dell'angolo esterno [EUCLIDE, XVII], avremo pure:

${\widehat {FIA}}+{\widehat {FICF}}>{\widehat {EA}}+{\widehat {FEC}}=$ 2 ${\widehat {retti}}$

E poichè si ha:

${\widehat {BAC}}+{\widehat {DCA}}>{\widehat {BAI}}+{\widehat {DCI}}$,

si deduce:

${\widehat {BAC}}+{\widehat {DCA}}>{\widehat {FIA}}+{\widehat {FIC}}>$ 2 ${\widehat {retti}}$

Allora, per l'uguaglianza dei due angoli ${\widehat {BAC}},<math>{\widehat {DCA}}$, si ricava:

${\widehat {BAC}}>$ 1 ${\widehat {retto}}$ c. d. d.

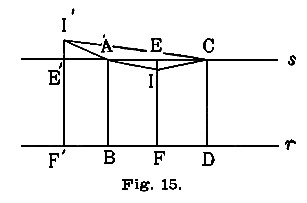
Supponiamo in secondo luogo $E'F'<AB$. Allora prolunghiamo $F'E'$ fino ad ottenere il segmento $F'I'=AB$ e congiungiamo $I'$ con $C$ ed $A$.

Valgono al solito le seguenti relazioni:

${\widehat {F'I'A}}={\widehat {BAI'}}$;

${\widehat {I'AE'}}>{\widehat {I'CE'}}$;

${\widehat {F'I'C}}={\widehat {DCI'}}$;

${\widehat {F'I'A}}<{\widehat {F'I'C}}$