| Questa pagina è stata trascritta e formattata, ma deve essere riletta. |
| 210 | intorno ad un’operetta di giovanni ceva. |
ed inoltre:
| 3) |
b + c : a = AO : A’O
c + a : b = BO : B’O a + b : c = CO : C’O. |
Dimostrazione. In causa delle (1) il centro di gravità comune de’ pesi applicati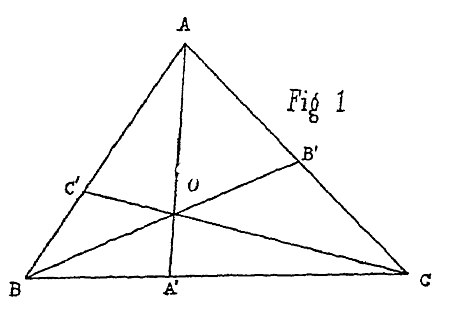 in A e B è C’, ed il centro dei pesi applicati in A e C è B’. Dunque il centro de’ tre pesi a, b, c dovrà cadere sì sulla C’C che sulla B’B, cioè sarà il punto O comune a queste due rette. Per conseguenza il centro de’ pesi b, c dovrà essere nella AO, ossia cadrà in A’. Dall’essere il centro de’ due pesi b + c ed a applicati l’uno in A’ e l’altro in A segue la prima delle relazioni (3). Analogamente si dica delle altre due.
in A e B è C’, ed il centro dei pesi applicati in A e C è B’. Dunque il centro de’ tre pesi a, b, c dovrà cadere sì sulla C’C che sulla B’B, cioè sarà il punto O comune a queste due rette. Per conseguenza il centro de’ pesi b, c dovrà essere nella AO, ossia cadrà in A’. Dall’essere il centro de’ due pesi b + c ed a applicati l’uno in A’ e l’altro in A segue la prima delle relazioni (3). Analogamente si dica delle altre due.
Se l’enunciato del precedente teorema si ristringe alla figura che risulta togliendo dalla 1.ª le rette AA’ e BC si ha l’elemento primo. Il quinto elemento può enunciarsi così:
Sui lati di un quadrigono qualsivoglia (piano o gobbo, convesso o concavo) ABCD (fig. 2.ª e 3.ª) si fissino quattro punti E, F, G, H in modo che fra i segmenti risultanti sussista la relazione seguente:
| 4) |
AE . BF . CG . DH = BE . CF . DG . AH
|
le rette EG, FH giaceranno sempre in uno stesso piano e si segheranno in un punto I. Se inoltre ai vertici del quadrigono si applichino quattro pesi a, b, c, d in modo che si abbia:
| 5) |
a : b = BE : AE, b : c = CF : BF, c : d = DG : CG
|
allora sarà inoltre:
| 6) |
d : a = AH : DH
|
e:
| 7) |
a + d : b + c = FI : HI, a + b : c + d = GI : EI.
|
Dimostrazione. Si moltiplichino fra loro, termine a termine, le proporzioni (5); risulterà:
a : d = BE . CF . DG : AE . BF . CG.
Ma la relazione (4) può scriversi anche così:
BE . CF . DG : AE . BF . CG = DH : AH

